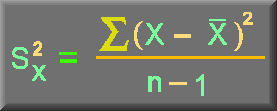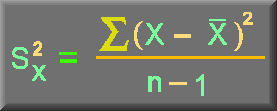Statisticians use the terms "degrees of freedom" to describe the number of values in the final calculation of a statistic that are free to vary. Consider, for example the statistic s-square.

To calculate the s-square of a random sample, we must first calculate the mean of that sample and then compute the sum of the several squared deviations from that mean. While there will be n such squared deviations only (n - 1) of them are, in fact, free to assume any value whatsoever. This is because the final squared deviation from the mean must include the one value of X such that the sum of all the Xs divided by n will equal the obtained mean of the sample. All of the other (n - 1) squared deviations from the mean can, theoretically, have any values whatsoever. For these reasons, the statistic s-square is said to have only (n - 1) degrees of freedom.