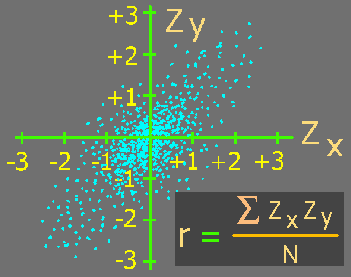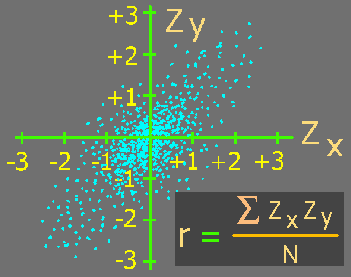Given a pair of related measures (X and Y) on each of a set of items, the correlation coefficient (r) provides an index of the degree to which the paired measures co-vary in a linear fashion. In general r will be positive when items with large values of X also tend to have large values of Y whereas items with small values of X tend to have small values of Y. Correspondingly, r will be negative when Items with large values of X tend to have small values of Y whereas items with small values of X tend to have large values of Y. The value of r is calculated by first converting the Xs and Ys into their respective Z Scores and, keeping track of which Z Score goes with which item, determining the value of the mean Z Score product. Numerically, r can assume any value between -1 and +1 depending upon the degree of the relationship. Plus and minus one indicate perfect positive and negative relationships whereas zero indicates that the X and Y values do not co-vary in any linear fashion.